Convergence order in trajectory estimation by piecewise-cubics and exponential parameterization
Abstract
This paper discusses the problem of estimating the trajectory of the unknown curve γ from the sequence of m+1 interpolation points .png) in arbitrary Euclidean space En . The respective knots
in arbitrary Euclidean space En . The respective knots 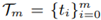 (in ascending order) are assumed to be unknown. Such Qm is coined reduced data. In our setting, a piecewise-cubic Lagrange interpolation
(in ascending order) are assumed to be unknown. Such Qm is coined reduced data. In our setting, a piecewise-cubic Lagrange interpolation 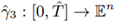 is applied to fit Qm. Here, the missing knots Ƭm are replaced by their estimates
is applied to fit Qm. Here, the missing knots Ƭm are replaced by their estimates 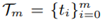 in accordance with the exponential parameterization. The latter is controlled by a single parameter λ ∈ [0, 1]. This work analyzes the intrinsic asymptotics in approximating γ by ŷ3 based on the exponential parameterization and Qm. The multiple goals are achieved. Firstly, the existing result established for λ = 1 (i.e. for the cumulative chord parameterization) is extended to the remaining cases of λ ∈ [0, 1) and more-or-less uniformly sampled Qm. As demonstrated herein, a quartic convergence order α(1) = 4 in trajectory estimation drops discontinuously to the linear one α(λ) = 1, for all λ ∈ [0, 1). Secondly, the asymptotics derived in this paper is also analytically proved to be sharp with the aid of illustrative examples. Thirdly, the latter is verified in affirmative upon conducting numerical testing. Next, the necessity of more-or-less uniformity imposed on Qm is shown to be indispensable. In addition, several sufficient conditions for ŷ3 to be reparameterizable to the domain of γ are formulated. Lastly, the motivation for using the exponential parameterization with λ ∈ [0, 1) is also outlined.
in accordance with the exponential parameterization. The latter is controlled by a single parameter λ ∈ [0, 1]. This work analyzes the intrinsic asymptotics in approximating γ by ŷ3 based on the exponential parameterization and Qm. The multiple goals are achieved. Firstly, the existing result established for λ = 1 (i.e. for the cumulative chord parameterization) is extended to the remaining cases of λ ∈ [0, 1) and more-or-less uniformly sampled Qm. As demonstrated herein, a quartic convergence order α(1) = 4 in trajectory estimation drops discontinuously to the linear one α(λ) = 1, for all λ ∈ [0, 1). Secondly, the asymptotics derived in this paper is also analytically proved to be sharp with the aid of illustrative examples. Thirdly, the latter is verified in affirmative upon conducting numerical testing. Next, the necessity of more-or-less uniformity imposed on Qm is shown to be indispensable. In addition, several sufficient conditions for ŷ3 to be reparameterizable to the domain of γ are formulated. Lastly, the motivation for using the exponential parameterization with λ ∈ [0, 1) is also outlined.
Keyword : interpolation, reduced data, convergence order and sharpness

This work is licensed under a Creative Commons Attribution 4.0 International License.
